នៅក្នុងធរណីមាត្រនៃយន្តហោះ រង្វង់មួយគឺជាសំណុំនៃចំណុចទាំងអស់ដែលមានលំនឹងពីចំណុចថេរ (ហៅថាកណ្តាល) នៅចម្ងាយដែលបានផ្តល់ឱ្យហៅថាកាំ។
កាំនៃរង្វង់ត្រូវតែជាលេខវិជ្ជមាន ធំជាង 0។
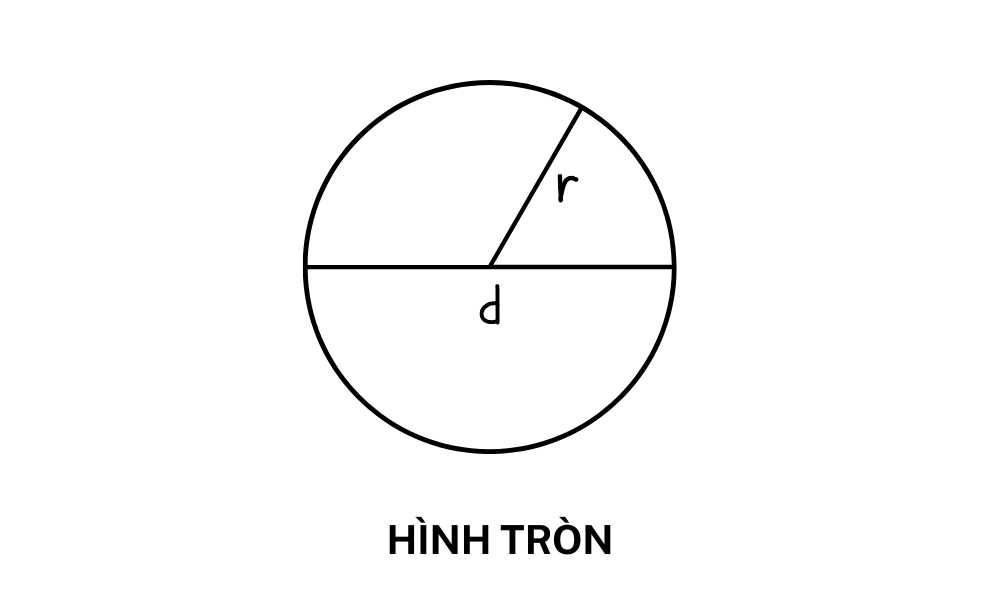
រង្វង់ និងរង្វង់គឺជាគំនិតពីរផ្សេងគ្នា។
រង្វង់គឺជាសំណុំនៃចំណុចទាំងអស់នៅខាងក្នុង និងនៅលើរង្វង់។ ម្យ៉ាងទៀត រង្វង់គឺជាផ្នែកឆ្លងកាត់ ដូច្នេះហើយមានផ្ទៃ។
រង្វង់គឺជាទីតាំងនៃចំណុចទាំងអស់នៅលើយន្តហោះដែលស្មើគ្នាពីចំណុចដែលបានផ្តល់ឱ្យ (ហៅថាកណ្តាល) - ខ្សែកោងបិទជិត (ដូចជាវណ្ឌវង្ក ព្រំដែន) មិនមានតំបន់ទេ។
តំបន់នៃរង្វង់មួយត្រូវបានគណនាដោយគុណការេនៃកាំដោយ pi ។
| S = rxrxnbsp;π = r 2 x π |
នៅទីនោះ៖
S: តំបន់នៃរង្វង់
r: កាំនៃរង្វង់មួយ - គឺជាចំងាយពីកណ្តាលរង្វង់ទៅចំនុចណាមួយនៅលើរង្វង់។
π (pi)៖ លេខ pi គឺជាចំនួនថេរគណិតវិទ្យា ប្រហែលស្មើនឹង 3.14159
នៅក្នុងគណិតវិទ្យា និងធរណីមាត្រ អង្កត់ផ្ចិតគឺជាផ្នែកបន្ទាត់ដែលឆ្លងកាត់កណ្តាលរង្វង់ ហើយភ្ជាប់ចំណុចទាំងពីរនៅលើរង្វង់។ អង្កត់ផ្ចិតគឺជាផ្នែកបន្ទាត់វែងបំផុតក្នុងរង្វង់មួយ ដោយបែងចែករង្វង់ជាពីរពាក់កណ្តាលស្មើគ្នា និងមានប្រវែងពីរដងនៃកាំ។
ចំពោះបញ្ហាដែលមានតែទិន្នន័យអង្កត់ផ្ចិត ប្រើរូបមន្តសម្រាប់គណនាផ្ទៃរង្វង់ដោយការ៉េ ½ អង្កត់ផ្ចិតគុណនឹង pi ។
| S = (d/2) 2 x π |
នៅទីនោះ៖
S: តំបន់នៃរង្វង់
ឃ: ប្រវែងអង្កត់ផ្ចិតរង្វង់
π (pi)៖ លេខ pi គឺជាចំនួនថេរគណិតវិទ្យា ប្រហែលស្មើនឹង 3.14159
រង្វង់នៃរង្វង់គឺជាប្រវែងនៃផ្លូវជុំវិញរង្វង់។ រូបមន្តសម្រាប់គណនាបរិមាត្រ (C) គឺ C = π xd (ដែល d ជាអង្កត់ផ្ចិត) ឬ C = 2 xrx π (ដែល r ជាកាំ) ។
ចំពោះបញ្ហាដែលមានតែទិន្នន័យរង្វង់ប៉ុណ្ណោះ មានវិធីពីរយ៉ាងក្នុងការគណនាផ្ទៃរង្វង់។
វិធីទី១៖ ប្រើរូបមន្តទូទៅ៖
| S = r 2 x π |
- ជំហានទី១៖ រកកាំ (r) ពីរង្វង់ (C)
រង្វង់រង្វង់គឺ C = 2 xrx π ដូច្នេះ r = C / (2π)
- ជំហានទី 2៖ អនុវត្តរូបមន្តដើម្បីគណនាផ្ទៃនៃរង្វង់មួយ។
ផ្ទៃនៃរង្វង់មួយគឺ S = r 2 x π ។ ជំនួស r ថ្មីដែលរកឃើញក្នុងជំហានទី 1 ហើយយើងមាន: S = (C/2π)² x π
បន្ទាប់ពីធ្វើឱ្យសាមញ្ញ យើងទទួលបានរូបមន្តចុងក្រោយ៖ S = (C) 2 /4π ។
វិធីទី ២៖ អនុវត្តរូបមន្តសាមញ្ញ ដើម្បីគណនាផ្ទៃរង្វង់ដោយបែងចែកការ៉េនៃរង្វង់ដោយ ៤ ដង pi៖
| S = (C) 2 /4π |
នៅទីនោះ៖
S: តំបន់នៃរង្វង់
C: រង្វង់នៃរង្វង់មួយ។
π (pi)៖ លេខ pi គឺជាចំនួនថេរគណិតវិទ្យា ប្រហែលស្មើនឹង 3.14159។
ផ្ទៃរង្វង់ត្រូវប្រើឯកតាផ្ទៃ (mm2, dm2, cm2, m2...)
កាំ អង្កត់ផ្ចិត រង្វង់មូល ត្រូវប្រើឯកតាប្រវែង (mm, dm, cm, m...)។
ប្រភព៖ https://vietnamnet.vn/cong-thuc-tinh-dien-tich-hinh-tron-la-gi-2441504.html





![[រូបថត] ប្រធានរដ្ឋ Luong Cuong ចូលរួមពិធីបើកបវេសនកាលឆ្នាំសិក្សាថ្មីនៅបណ្ឌិតសភាការពារជាតិ](https://vphoto.vietnam.vn/thumb/1200x675/vietnam/resource/IMAGE/2025/9/15/c65f03c8c2984e60bd84e6e01affa8a0)

![[រូបថត] អគ្គលេខាធិកា To Lam ធ្វើជាអធិបតីក្នុងកិច្ចប្រជុំការងារជាមួយគណៈកម្មាធិការអចិន្ត្រៃយ៍នៃគណៈកម្មាធិការបក្សនៃក្រសួងការបរទេស](https://vphoto.vietnam.vn/thumb/1200x675/vietnam/resource/IMAGE/2025/9/15/f26e945b18984e8a99ef82e5ac7b5e7d)






















![[រូបថត] អគ្គលេខាធិកា To Lam ចូលរួមក្នុងខួបលើកទី 80 នៃអគ្គនាយកដ្ឋានឧស្សាហកម្មការពារជាតិ](https://vphoto.vietnam.vn/thumb/1200x675/vietnam/resource/IMAGE/2025/9/15/fb8fd98417bb4ec5962de4f7fbfe0f6a)





































![[ផ្សាយផ្ទាល់] ពិធីបិទពិព័រណ៍សមិទ្ធិផលជាតិ "៨០ឆ្នាំនៃដំណើរឯករាជ្យ-សេរីភាព និងសុភមង្គល"](https://vphoto.vietnam.vn/thumb/402x226/vietnam/resource/IMAGE/2025/9/15/de7064420213454aa606941f720ea20d)































Kommentar (0)